quadratische Gleichungen

Gleichungen Lösen - das gehört zum grundlegenden Handwerkszeug.

Bei quadratischen Gleichungen gibt es zum Glück eine Art Universalschlüssel:
Mit quadratischer Ergänzung kann man jede Gleichung des Typs
$$x^2+b\cdot x+c=0.$$ lösen
Oder man kann die p-q-Formel benutzen, eine Art Ersatzschlüssel.
Eigentlich brauchen wir also nur diesen einen Schlüssel - warum sollte man sich weitere Verfahren auch nur ansehen?

Na ja, vielleicht liegt die Gleichung, um die es geht, ja in einer anderen Form vor und sieht z.B. so aus:
(leicht abgeändert gegenüber dem Original) $$(x-5)^2-4=0.$$
Und dann bietet sich ein anderes Vorgehen an.

Außerdem kann man aus anderen Wegen einfach etwas lernen - dann können wir am Ende noch viel mehr als nur quadratische Gleichungen lösen ...
In diesem Sinne: los geht´s:

Die faktorisierte Form: zwei Klammern - ein Geschenk.

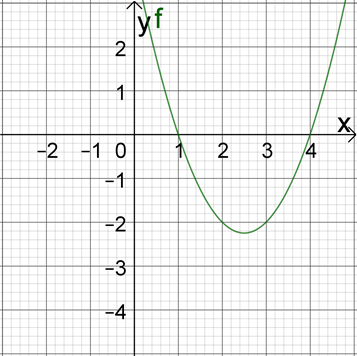
$$(x-1)(x-4)=0.$$

In diesem Fall kommt man ganz ohne Rechnen aus, allein durch Herumdrehen der Vorzeichen!

Beispiel

Training (ein paar Aufgaben, damit man´s grundsätzlich drauf hat)

Check (hier werden auch ein paar Schwierigkeiten ausgelotet)

Übersicht faktorisierte Form bei quadratischen Funktionen: pdf

Ausklammern.

c=0? Dann mach dir selbst ein Geschenk!



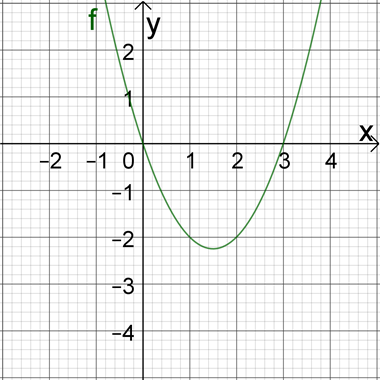
$$x^2-3x=0.$$


Wenn der y-Achsenabschnitt Null ist, kannst du x ausklammern. Dann stehen die Lösungen wieder fast da!
Beispiel
Training (ein paar Aufgaben, damit man´s grundsätzlich drauf hat)
Check (hier gibts ein paar Variationen)

Check ganzrational (hier werden auch ein paar Funktionen untersucht, nicht nur quadratische)
Check faktorisierte Form bei quadratischen Funktionen: pdf

x²+c=0

Der symmetrische Sonderfall.


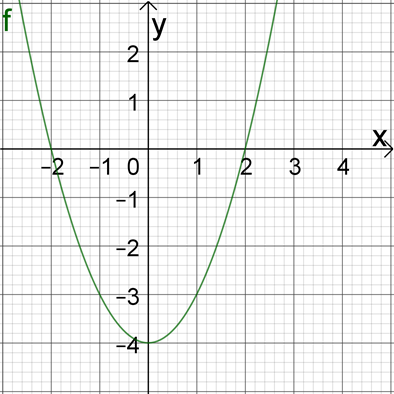
$$x^2-4=0.$$

Wenn b=0 ist, reicht: Plus und Wurzel!

Beispiele: Beispiel 1 ,
Beispiel 2 ,
Beispiel 3
Check

Die Scheitelpunktform: eins nach dem andern ...

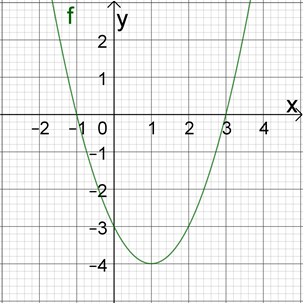
$$(x-1)^2-4=0.$$

Hier kann man die Gleichung Schritt für Schritt abarbeiten, indem man die passende Umkehr-Operation anwendet: erst +4, dann die Wurzel ziehen und dann +1.

Übersicht Scheitelpunktform: pdf

Check Scheitelpunktform: pdf

Quadratische Ergänzung: das Verfahren, das immer geht.

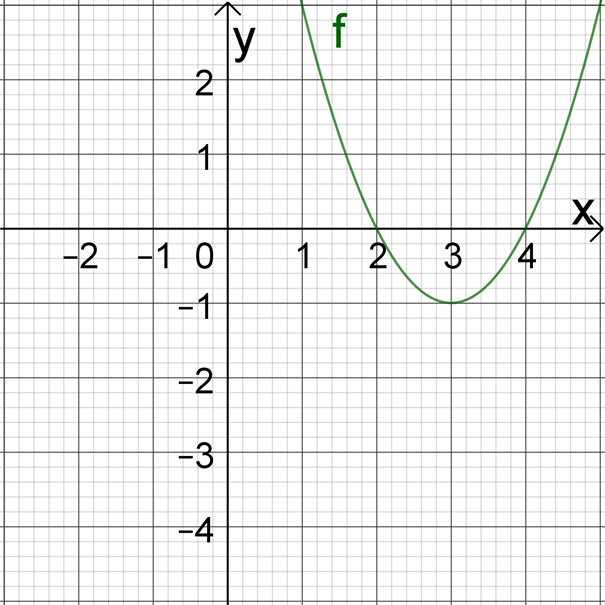
$$x^2-6x+8=0.$$




Erklärfilm quadratische Ergänzung mp4

Erklärfilm zum interaktiven Training quadratische Ergänzung youtube

Hinweis: damit gehst du auf youtube

interaktives Training: quadratische Gleichungen lösen (\(x^2+bx+c=0\)) (nur Normalparabeln)

interaktives Training: quadratische Gleichungen lösen (\(ax^2+bx+c=0\)) (auch gestreckte und gestauchte)

interaktives Training: quadratische Gleichungen lösen (\(a_1x^2+b_1x+c_1=a_2x^2+b_2x+c_2\)) (auch gestreckte und gestauchte)

Check quadratische Ergänzung:
erstmal ohne Faktor vor dem x²:pdf,
dann mit pdf
und nochmal: pdf

Jetzt nochmal alles:

Check quadratische Gleichungen (alle Formen) mit Links zu Lösungen: pdf
und noch eine pdf


Check Schnittpunkte quadratischer Funktionen: pdf



Standardaufgaben quadratische Gleichungen (Beispiele und Lösungen): quadratische Gleichung, faktorisiert, quadratische Gleichung der Form ax^2+c=0, noch eine der Form ax^2+c, eine der Form ax^2+bx=0, eine der handelsüblichen Form ax^2+bx+c=0, eine der Form ax^2+bx+c=dx^2+ex+f (Schnittstellenbestimmung), quadratische Gleichung mit Parameter

Für die Übersicht, was man in diesem Zusammenhang alles können kann,
gibt es Checklists mit Links zu Trainingsmöglichkeiten:

Checklist quadratische Gleichungen: pdf