mehr als nur 3D: Die Matrizenrechnung ...

... ist in vielen Bereichen nützlich, in denen lineare Zusammenhänge zwischen mehreren Größen bestehen:
Produktionsverflechtungen oder Entwicklungen zwischen verschiedenen Zuständen
- ob es sich um die verschiedenen Altersgruppen einer Bevölkerung mit ihrer jeweiligen Anzahl handelt oder die Anzahl verschiedener Panini-Bildchen, die ein Sammler inzwischen hat, mit der zugehörigen Übergangswahrscheinlichkeit, ein neues Bild zu ergattern.

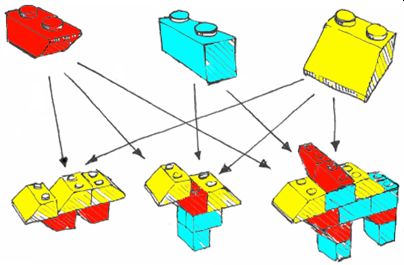
Matrizenrechnung lässt sich auf viele Felder anwenden,
darunter die Berechnung des Materialbedarfs bei mehrstufigen Produktionsprozessen, Lineare Optimierung und das Stellen von Prognosen mit Hilfe von Übergangsmatrizen.

Einfach gesagt ist Matrizenrechnung der mathematische Umgang mit "Zahlen im Paket",
Matrizen sind in diesem Sinne Tabellen, mit denen man rechnen kann.


Das klingt erstmal recht einfach - und das ist es auch. Nur zur Einführug der Grundbegriffe eine kleine Einführung: Tabellen für Materialflüsse

Eine ganz neue Art Malzunehmen

Zum Einstieg kann man sich am besten einen zweistufigen Produktionsprozessen anschauen: Die LEGO-Figuren und Die Spielzeug-Eisenbahn

Wie du gesehen hast, kann man Produktionsverflechtungen (also Mengenangaben, wieviel man wovon braucht) durch Matrizen angeben oder durch Graphen - die sogenannten Gozintographen.
Der Zusammenhang zwischen beiden hier im Video: M P (auf youtube)
oder auch bei Daniel Jung (auf youtube)

Nach diesem Einstieg lohnt es sich, die Matrizenmultiplikation genauer zu betrachten
und mit dem Falk´schen Schema übersichtlicher zu machen.

Nun ist es Zeit für ein paar Definitionen

Irgendwann merkt man dann, dass die Matrizenmultiplikation nicht immer so funktioniert, wie erwartet:

Das alles nochmal im Video: MathemaTrick (auf youtube) Besonderheiten der Matrizenmultiplikation

Mehrstufige Produktionsprozesse im Video:
erstmal die Basics: Mathe allein zuhaus (auf youtube)

Fit im Mathe-Abi (auf youtube)

Training grundlegend: mathestunde (pdf)

Teilen geht nicht - was geht dann? - LGS

Hanteln zusammenbauen: Hinführung zu Linearen Gleichungssystemen

Training LGS: Training

Unterschiede in der Lösbarkeit von LGS: Glossar LGS

Unterschiede in der Lösbarkeit von LGS: obere Dreiecksmatrizen

Check LGS: Check

Zu Linearen Gleichungssystemen gibt es auch eine eigene Seite!

Der Generalschlüssel: Die Inverse (wenn es sie gibt)

Training Inverse

Die Inverse: Check

FAQ: Warum kann man eigentlich nicht durch Matrizen teilen?

Übersicht gewinnen und Training

mehrstufigen Produktionsprozesse

Übersicht mehrstufige Produktionsprozesse

Schulbuch mit Übersichten und vielen Trainingsaufgaben: Bildungsverlag Eins

gute Übersicht: Auszug aus Schulbuch: Merkur Verlag

zweistufige Produktionsprozesse (Bsp. 1)

zweistufige Produktionsprozesse (oHiMi) - heri kommt zwar eine Inverse vor, wenn man noch nicht Interterien kann, lohnen sich vielleicht die andern Teilaufgaben ...

zweistufige Produktionsprozesse (oHiMi)

Standardaufgaben mit Lösungen: Berufskolleg Kaufmännische Schulen Kreis Düren (pdf)


Check, was du kannst!

Grundtechnik 1: Check Matrizenmultiplikation


Check Inverse


Check Ansätze zweistufiger Produktionsprozess

Check zweistufiger Produktionsprozess

Zur Überprüfung, was du alles können kannst: Checklist Matrizenrechnung

Was man sonst noch so mit Matrizen veranstalten kann:

Geometrisches

z.B. Drehmatrizen und Projektionsmatrizen (sehr geeginet für Schattenwurf)

Check Drehmatrizen

Check Projektionsmatrizen

Übergangsmatrizen und Markov-Prozesse

02_markov_mindmap-freeware.pdf
03_markov_stationaere_verteilungen.pdf
04_markov_kaeferaufgabe.pdf
05_wenige_radioaktive_atome.pdf
06_markov_google_pagerank_stoch_mit_matrizen.pdf 08_markov_kategorien_2.pdf
09_markov_katz_und_maus.pdf 10IQB AUfgabe CAS
11_markov_travelbugs.pdf
Roolfs: pdf mit jeder Menge interessanter Aufgaben (42 Seiten)
Checklist Markov
Geogebra Datei zu Markov-Prozessen

Lineare Optimierung

Checklist Lineare Optimierung


Glossar grundlegender Begriffe: Matrizenrechnung, Matrix, Format einer Matrix, quadratische Matrix, Matrizenmultiplikation, inverse Matrix, Determinante.